جاوب واسال

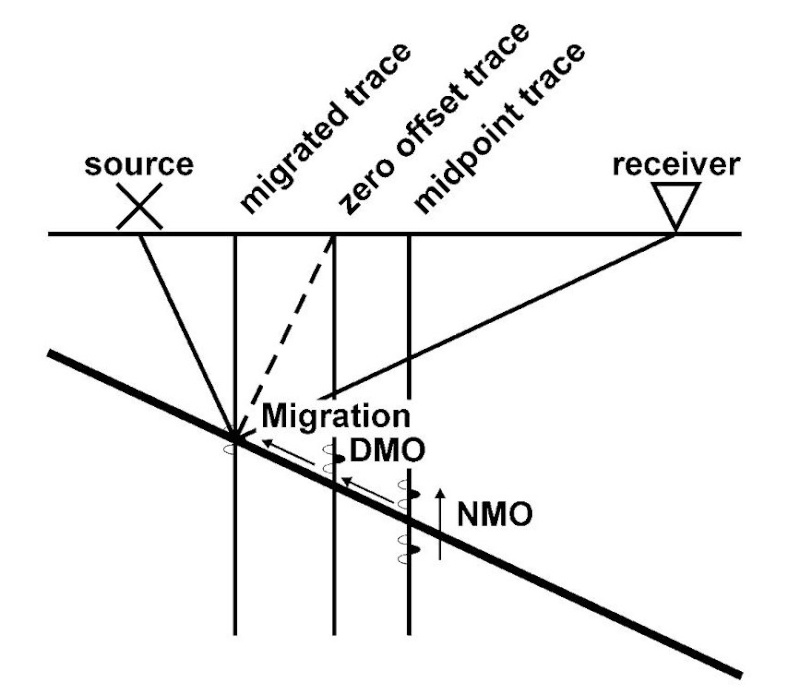
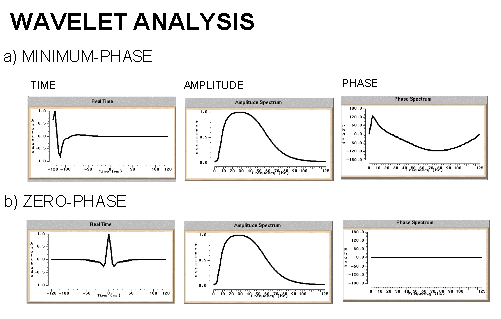
both are wave phases results from the energy souce zero phase wavelet is symmetric on the origin and it is produced from vibrosis
minimum phase is a wave with zero amplitude at the origin it is produced from other sources of energy
for processing all waves must be in minimum phase
The minimum phase wavelet has a short time duration and a concentration of energy at the start of the wavelet. It is zero before time zero (causal). An ideal seismic source would be a spike (maximum amplitude at every frequency), but the best practical one would be minimum phase. It is quite common to convert a given wavelet source wavelet into it's minimum phase equivalent since several processing stages (e.g. predictive deconvolution) work best by assuming that the input data is minimum phase. The maximum phase wavelet is the time reverse of the minimum phase and at every point the phase is greater for the maximum than the minimum. All other causal wavelets are strictly speaking mixed-phase and will be of longer time duration. The convolution of two minimum phase wavelets is minimum phase. The zero-phase wavelet is of shorter duration than the minimum phase equivalent. The wavelet is symmetrical with a maximum at time zero (non-causal). The fact that energy arrives before time zero is not physically realisable but the wavelet is useful for increased resolving power and ease of picking reflection events (peak or trough). The convolution of a zero-phase and minimum phase wavelet is mixed phase (because the phase spectrum of the original minimum phase wavelet is not the unique minimum phase spectrum for the new modified wavelet) and should be avoided



and now the question is what are the types of core analysis?

Excellent answer moony

The Major Types of Core Analysis

• Plug (Conventional) Analysis
  
  
  
  • Consolidated Formations
    
  • UnconsolidatedFormations
    


• Full-Diameter Analysis
  
  
  
  • Routine Analysis
    
  • Pressure Core Analysis
    
  • Sponge Core Analysis
    


• Sidewall Core Analysis
  

1. Plug (Conventional) Analysis

a. Consolidated Formations


This technique is normally
restricted to homogeneous formations that can be characterized with plug-size
samples. Typical plug size is 1 inch (2.5 m) in diameter, and 1 inch (2.5 cm)
long.

b. Unconsolidated Formations

Unconsolidated
sand recovered within a rubber sleeve core barrel, a plastic inner barrel
liner, or a fiberglass barrel is often stabilized by freezing prior to
sampling. Frozen interstitial water present at the grain contacts immobilizes
the rock particles. Plugs are drilled using liquid nitrogen as the bit
lubricant.

2. Full Diameter Analysis
a. Routine Analysis

Full
diameter analysis was introduced to allow testing of rocks with complex
lithology, such as heterogeneous carbonates and fissured, vugular formations
unsuitable for plug analysis.

b. Pressure Core Analysis

The analysis of full diameter
pressure cores follows, in a modified form, the procedures normally employed in
more routine analysis. Full diameter samples are cut in the form of a right
cylinder and then placed in specialized, airtight containers where they thaw,
so that fluids expulsed from the core can be collected and measured.

c. Sponge Core Analysis

Full diameter analysis of
samples recovered within the sponge barrel proceeds along the usual lines once
the core has been removed from the barrel. The sponge itself is cut from the
core barrel and the fluids it contains are extracted using a vacuum retort
technique. Both oil and water volumes within the sponge are measured.

3. Sidewall Core Analysis


Sidewall samples are used extensively
in softer sand areas. (Note, however, that a sidewall-drilled plug from a new
sidewall coring device can be used for harder formations and can be analyzed in
the same manner as a standard plug-sized core.) Percussion sidewalls are often
smaller and demand additional attention.



Now Easy Question



What is the Ground roll??

Exxxxxcellent answer my Friend Hossny


انتا ديما يا حسنى عند حسن الظن